Activation Functions
Review:
Activation functions used after the weights and bias are multipled and added together, produces the output of that neuron
Types of Activation Functions
Binary Step Function
Has threshold
If input > or < threshold => sends exactly the same signal to next layer
Produces 1 or 0 (passed threshold or not)
So does not allow multi-value output (classification)
Linear Activation Function
Aka linear regression model
Creates output (after multiplying and adding weights and bias) that is linearly proportional to input
Allows multi-value output
Cannot use backpropogation
Derivative of function is a constant (Constant has no relation to input X)
Cannot backtrack to see how weights can improve to minimize loss
Basically only has 2 layers (input -> output)
Since it's linear output, any layers added don't change the fact that any output is just linear to the input
Non-Linear Activation Function
Allows backpropogration
Derivatives are related to input
Allows for multiple layers
Common Non-Linear Activation Functions
Sigmoid / Logistic

Pros:
Smooth gradient (prevents "jumps" in output values)
Bounded output values for each neuron () by normalization
Clear predictions
If , is very close to either 0 or 1 (Refer to graph)
Cons:
Vanishing Gradient Problem
High or low X values are indistinguishable since they just round back to 0 or 1
Makes network unable to learn more
Predicting can be slow
Computationally expensive
Output is not zero-centered (sigmoid only outputs values between 0 and 1, 0 is clearly not the center)
Refer to this link for explanation on why that's bad
TanH / Hyperbolic Tangent:

Pros:
Zero-centered
like sigmoid
Cons:
Like sigmoid
ReLU (Rectified Linear Unit)
if
if

About:
Only used for hidden layers (not output layer)
Linear for anything greater than 0
0 for anything less than 0
Pros:
Computationally efficient (converges quickly)
No vanishing gradient problem
Cons:
Not zero-centered
The Dying ReLU problem
If neuron outputs negative value, the output is 0. This is hard to recover from since the derivative of 0 is just 0 (unlikely for neuron to recover).
i.e. Non-differetiable at 0 (cannot perform backpropagation)
Not usually used in RNNs
RNNs output very large values, and ReLU does not bound output values, so you could have exploding gradient problem
Leaky / Parametric ReLU / Maxout Function
if
if
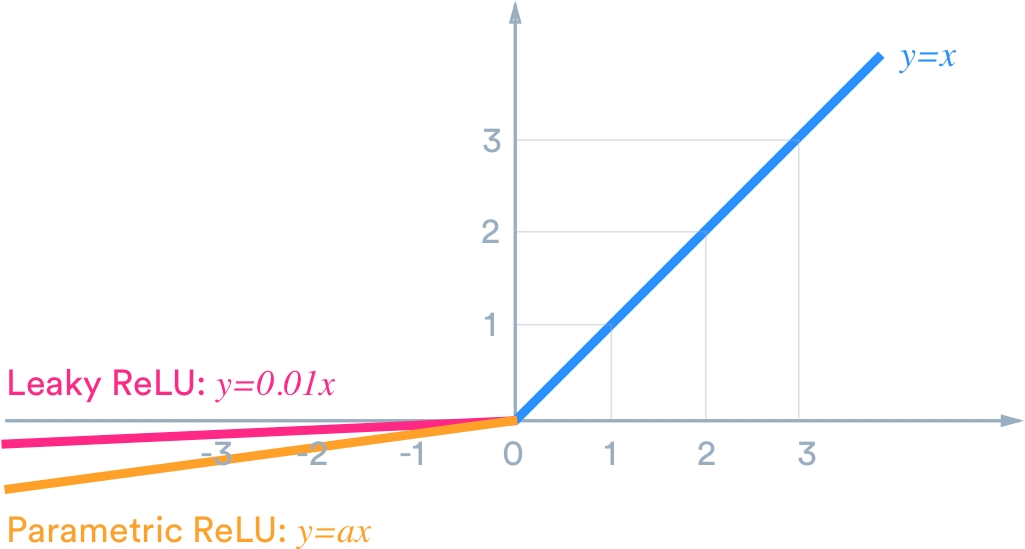
About:
is a parameter
for leaky Relu
Pros:
Fixes "dying relu problem" (no 0 slope, so can have backpropagation now)
Speeds up training
Cons:
Results not consistent for negative values
You have to tune the slope parameter
Softmax
About:
No graph because Softmax is a multivariable function
Multi-class classification version of Sigmoid
Sigmoid and Softmax are the same in binary classification
Pros:
Can handle multiple classes (Useful for output neurons)
Normalizes outputs for each class between 0 and 1, then divides by sum
Gives probability of input being in specific class
Last updated
Was this helpful?